On Computable Numbers, with an Application to the Entscheidungsproblem

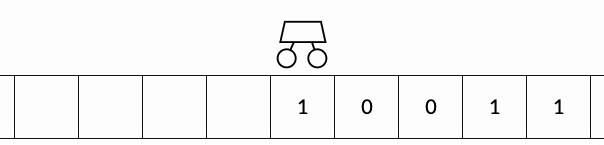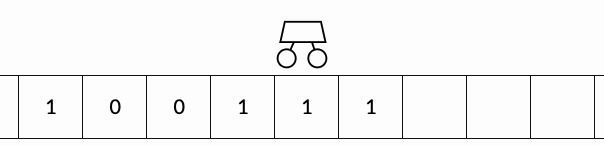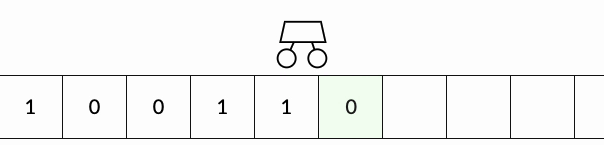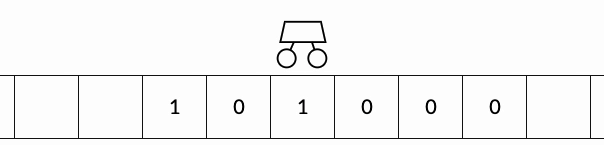
This visualisation shows a Turing Machine with a simple set of rules incrementing 39 to 40 in binary. Source: Medium.

Abstract

The “computable” numbers may be described briefly as the real numbers whose expressions as a decimal are calculable by finite means. Although the subject of this paper is ostensibly the computable numbers. it is almost equally easy to define and investigate computable functions of an integral variable or a real or computable variable, computable predicates, and so forth. The fundamental problems involved are, however, the same in each case, and I have chosen the computable numbers for explicit treatment as involving the least cumbrous technique. I hope shortly to give an account of the relations of the computable numbers, functions, and so forth to one another. This will include a development of the theory of functions of a real variable expressed in terms of computable numbers. According to my definition, a number is computable if its decimal can be written down by a machine…

Note: This is an example of a Jekyll-based project website template: Github link.
The following content is generated by ChatGPT. The figure is manually added.

Background

The paper “On Computable Numbers, with an Application to the Entscheidungsproblem” was published by Alan Turing in 1936. In this groundbreaking paper, Turing introduced the concept of a universal computing machine, now known as the Turing machine.

Objective

Turing’s main objective in this paper was to investigate the notion of computability and its relation to the Entscheidungsproblem (the decision problem), which is concerned with determining whether a given mathematical statement is provable or not.

Key Ideas

Turing first presented the concept of a “computable number,” which refers to a number that can be computed by an algorithm or a definite step-by-step process.
He introduced the notion of a Turing machine, an abstract computational device consisting of an infinite tape divided into cells and a read-write head. The machine can read and write symbols on the tape, move the head left or right, and transition between states based on a set of rules.
Turing demonstrated that the set of computable numbers is enumerable, meaning it can be listed in a systematic way, even though it is not necessarily countable.
He proved the existence of non-computable numbers, which cannot be computed by any Turing machine.
Turing showed that the Entscheidungsproblem is undecidable, meaning there is no algorithm that can determine, for any given mathematical statement, whether it is provable or not.

Turing Machine

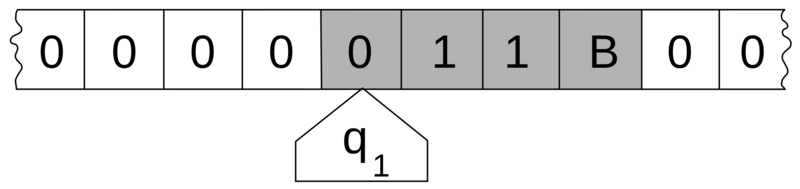
Figure 1: A representation of a Turing Machine. Source: Wiki.

A classic Turing machine illustration.

Placeholder slide for results.

Table: Comparison of Computable and Non-Computable Numbers

Computable Numbers	Non-Computable Numbers
Rational numbers, e.g., 1/2, 3/4	Transcendental numbers, e.g., π, e
Algebraic numbers, e.g., √2, ∛3	Non-algebraic numbers, e.g., √2 + √3
Numbers with finite decimal representations	Numbers with infinite, non-repeating decimal representations

He used the concept of a universal Turing machine to prove that the set of computable functions is recursively enumerable, meaning it can be listed by an algorithm.

Significance

Turing’s paper laid the foundation for the theory of computation and had a profound impact on the development of computer science. The Turing machine became a fundamental concept in theoretical computer science, serving as a theoretical model for studying the limits and capabilities of computation. Turing’s work also influenced the development of programming languages, algorithms, and the design of modern computers.

Citation

@article{turing1936computable,
  title={On computable numbers, with an application to the Entscheidungsproblem},
  author={Turing, Alan Mathison},
  journal={Journal of Mathematics},
  volume={58},
  number={345-363},
  pages={5},
  year={1936}
}